Objective: to Assess the Euler’s buckling load of strut
Equipment and Tools
- Venire Caliper Scale
- Strut Testing Apparatus
Description of Equipment
The machinery equipment is designed in such a way that it is enabled to carry out tests on struts of wide assortment of lengths, of which the ends are either hinged or joined. The equipment comprises of a rectangular durable framework with weighty cast iron foundation. The crest and the base end of the strut under the test are held in sockets focally positioned on the crest cross arm and the base correspondingly. The cross- arm is adaptable to ease lodging of strut of numerous lengths not exceeding 1m. The shift of the top socket in the guide of top cross- arm with least amount of friction leads to the effectual utilization of the axial loads. The utilization of axial load is created by augmenting weights on the hanger mounted on the crest socket. The deflection of the strut changes each one of the loading is minutely calculated by a micrometer attached to an adaptable stage. Greater precision of dimension is confirmed by a pointer lamp which g lows when the micrometer arm is attuned to come in contact with the swerved strut.
Theory and Principle
In all the cases of unusually long columns, the failure occurs chiefly because of the bending. The Euler’s relations provide the crippling load for long columns for different end condition.
Crippling Load,
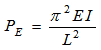
Where E = Modulus of Elasticity of the material (2.1 x l0^5N/mm^2)
I = Moment of Inertia of the cross Section of the strut (mm^4)
Where D= diameter of the strut.
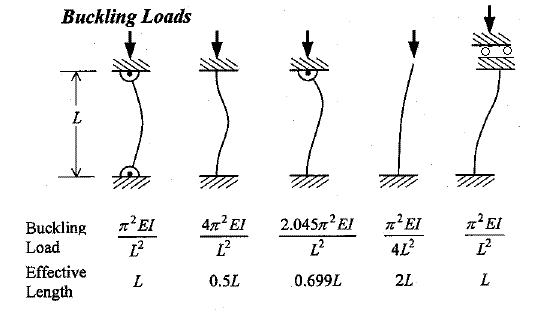
L = Effective length orate strut.
= L when both ends are hinged
= L/2 When the ends are connected
![]() when one end fixed and other end hinged.
when one end fixed and other end hinged.
= 2L when one end fixed and other end free.
(Where L is the total length of the strut)
Process
First of all, clean the strut thoroughly with sand paper. Regulate the rope slide so that it suits the length of the strut and position the strut amongst the top and bottom adapter. To conduct tests with hinged end, two balls are specified which is given, and additionally which has to be tightened properly to make sure of the end fixity. Shift the side sliding block so that the micrometer strut is almost against the median of the longitude of the strut and clamp it tightly. Now regulate the micrometer Sliding holder, so that the micrometer occurs precisely at the midpoint of the strut. Now, position the weight hanger on the top of the socket such that the loading is only axial. Turn the switch `on’ so that every time the micrometer traces the strut the indicator lamp lights up. Meticulously spinning the strut with fingers with help of one revolution, the maximum and minimum readings of the micrometer are marked down and noted. The objective of this is to assess the direction of curvature of the strut and also to receive the amount of original curvature.
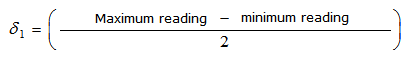
Where ![]() refers to the original deflection of strut beneath on load and deflection of strut because of the weight of the hangers 2kg. The strut should be positioned in such a way the original curvature is distant from the micrometer side. First regulate the original reading of the micrometer with the original curvature away from the micrometer.
refers to the original deflection of strut beneath on load and deflection of strut because of the weight of the hangers 2kg. The strut should be positioned in such a way the original curvature is distant from the micrometer side. First regulate the original reading of the micrometer with the original curvature away from the micrometer.
Now, add weights (in step of l kg) load on both of the sides of hanger so that the strut curves in the course away from the micrometer and mark down the reading. The difference between the two readings provides the accurate deflection because of the weights now augmented. Don’t rotate or revolve the strut while augmenting loads because the strut has to be kept in such a way that the curvature is pointing the same direction all the time.
Graphs
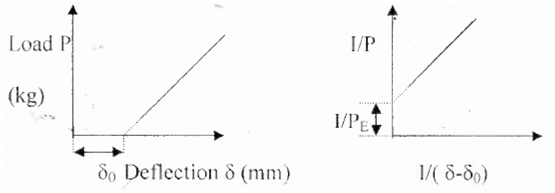
A graph of load P Vs. deflection ![]() is neatly plotted in a graph (
is neatly plotted in a graph ( ![]() being the aggregate deflection of the strut when a specific load is applied). From the graph deflection of the strut under on load
being the aggregate deflection of the strut when a specific load is applied). From the graph deflection of the strut under on load ![]() is found out.
is found out.
Subtracting ![]() from
from ![]() , the real deflection for each load. i.e. , (
, the real deflection for each load. i.e. , ( ![]() –
– ![]() ) can be calculated and draw a graph between 1/ (
) can be calculated and draw a graph between 1/ ( ![]() –
– ![]() )and I/P
)and I/P
For bulking load
![]()
i.e.
![]()
i.e., the value of I/P at ![]() , corresponds to the reciprocal of the bulking load . Now, calculate the bulking load from this (experimental outcomes).
, corresponds to the reciprocal of the bulking load . Now, calculate the bulking load from this (experimental outcomes).
Calculation
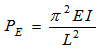
Result
1. By Eulers formula = ___________N
2. Experimental Values= _________N
Questions
- What is meant by buckling
- Name the various modes of failure of columns
- State the limitations of Euler’s formula
- Define Slenderness ratio.
- Name the best cross section for a column. Give reasons.
- State the difference between strut and column